Orpheus의 기초음악 이론을 시작하며...
(1) 내 스스로는 내가 지금까지 알고 있는 지식들을 정리하며
(2) 또 제 블로그에 찾아주신 여러분들께는음악을 연주하거나 MIDI를 접하게 되면서,
연주, 작곡, 편곡을 해나갈때 도움이 되었으면 하는 바람으로 시작합니다.
(3) 음악 비전공자이기 때문에 내용상 틀린 부분이 있을 수 있습니다. 피드백 부탁드립니다.
(4) 악보 그림위에 마우스를 올리거나, 클릭하면 악보의 연주 또는 악보의 설명이 있습니다.
다음 시간으로 가기 Orpheus의 기초음악이론 2. - 음정(2) "자리바꿈 음정의 계산"
음정 (1) "음정의 정의와 계산"
1. 음정이란?
- 정의 : 악보 표기 상에서 한 음과 다른 음 사이의 음높이의 차이
- 선율적 음정 : 순차적으로 소리가 나는 경우의 음정
- 화성적 음정 : 동시에 소리가 나는 경우의 음정
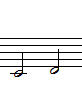

그림 1-1. 선율적 음정 그림 1-2. 화성적 음정
2. 음정의 계산 방법
(1) 첫 단계
- 무조건 다장조로 생각하기 (무조건 # 이나 b 없애기)
- 동일 음정은 1도, 악보 상에서 차례대로 1도씩 증가.
- 두 음 중 아래쪽에 있는 음을 기본으로 계산하기
그림 2-1.
1도 2도 3도 4도 5도 6도 7도 8도 9도
예제 1.
#이나 b이 없다면 모두 "도~레" 로 생각할 수 있으므로 전부 2도 관계임
(2) 두번째 단계
- 완전, 장, 단, 증, 감이란 말 붙여보기
- 이를 위해서는 우선 다장조에서 기본음인 "도"를 중심으로 알아보기
완전 1도 장 2도 장 3도 완전 4도 완전 5도 장 6도 장 7도 완전 8도 장 9도
* 1 2 3 4 5 6 7 의 앞에 말을 붙이면
* 완장장 완완 장장 이 됩니다.
* 세로줄로 읽으면 1완 -> 즉, 완전 1도
2장 -> 즉, 장 2도
* 도~파의 계산은 도부터 따져서 레(2도), 미(3도), 파(4도) 이므로 4도 관계이고,
1 2 3 4
완장장 완 이므로 완전 4도가 됩니다.
* 8도를 넘어가도 완장장~~~~ 식으로 나간다고 생각하면 완전 8도, 장9도가 됩니다.
(3) 세번째 단계
- 완전, 장에서 온음과 반음이 각각 몇개씩인지 알아보기
- 온음 한개는 반음 두개가 합쳐진 것과 같습니다.
- "미~파" 사이는 반음 1개로 진행, "시~도"사이도 마찬가지로 반음 1개로 진행됩니다.
표 1.
* 음정 온음 개수 반음 개수 sum : 온음을 2, 반음을 1로 계산하면
도도 완전 1도 0 0 0
도레 장 2도 1 0 2
도미 장 3도 2 0 4
도파 완전 4도 2 1 5
도솔 완전 5도 3 1 7
도라 장 6도 4 1 9
도시 장 7도 5 1 11
도도 완전 8도 5 2 12
(4) 네번째 단계 (Final)
- 완전, 장, 단, 증, 감, 겹증, 겹감의 관계 알아보기
- 완전 1,4,5,8 도에서는 두 음 사이의 거리가 반음만큼 더 멀어지면 "증",
반음만큼 더 가까워지면 "감"이됩니다.
표 2.
sum의 변화
또는 -1 -1 +1 +1
반음 개수의 변화
겹감 <-- 감 <-- 완전 --> 증 --> 겹증


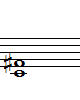
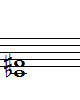
그림 2-2. 감 4도 완전 4도 증 4도 겹증 4도
(반음 좁아짐) (반음 멀어짐) (증 4도에서 또 반음 멀어짐)
예제 2-1. (답은 그림에 마우스 올리시면 나타납니다.)
- 장 2,3,6,7 도에서는 두 음 사이의 거리가 반음만큼 더 멀어지면 "증",
반음만큼 더 가까워지면 "단"이됩니다
- 단 2,3,6,7 도에서는 두 음 사이의 거리가 반음만큼 더 멀어지면 "장",
반음만큼 더 가까워지면 "감"이됩니다
표 3.
sum의 변화
또는 -1 -1 +1 +1
반음 개수의 변화
겹감 <-- 감 <-- 단 <--> 장 --> 증 --> 겹증
그림 2-3. (1) 파~라 이므로 우선 3도 관계의 음
(2) 파~솔, 솔~라 사이는 각각 온음 하나씩 움직인다.
그러므로 파~라까지는 온음 2개이므로, 표1에 의해 파~라는 장3도이다.
(3) 위의 음 라에 #이 붙어서 반음만큼 사이가 멀어지므로 증 3도이다.
그림 2-4. (1) 미~솔이므로 우선 3도 관계의 음
(2) 미~파는 반음, 파~솔은 온음으로 움직인다.
표1. 에 의해 장 3도는 온음이 두개일 때이다. 그런데,
반음만큼 두 음 사이가 가까워졌으므로, 단 3도
예제 2-2. (답은 그림에 마우스 올리시면 나타납니다.)
예제 2-3. (답은 그림에 마우스 올리시면 나타납니다.)
(5) 이명동음적 음정
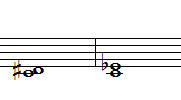
그림 2-4. 레# 과 미b은 실제로 같은 소리가 나는 음이다.
다만 악보상에서 "도~레#" 과 "도~미b"은 다른 음정이다.
도~레# : 증 2도
도~미b : 단 3도
- 표 1. 을 다시 한 번 확인해 보자.
- 장 2도는 sum 이 2, 반음만큼 사이가 더 늘어난 증 2도는 2 + 1 을 해서 sum3 이 된다.
- 장 3도는 sum 이 4, 반음만큼 사이가 더 줄어든 단 3도는 4 - 1 을 해서 sum3 이 된다.
- 이렇게, 다른 이름의 음정을 같고 있지만, 실제 연주에서 같은 음이 나오게 되는 음정을
이명동음적 음정이라고 한다.
표 1.
* 음정 온음 개수 반음 개수 sum : 온음을 2, 반음을 1로 계산하면
도도 완전 1도 0 0 0
도레 장 2도 1 0 2
도미 장 3도 2 0 4
도파 완전 4도 2 1 5
도솔 완전 5도 3 1 7
도라 장 6도 4 1 9
도시 장 7도 5 1 11
도도 완전 8도 5 2 12
3. 문제
(1) 다음 두 음의 음정을 계산하시오.
(2) 다음 두 음의 음정을 계산하시오.
* 본문 중의 "sum"이라는 용어는 음정 관계를 수적으로 표현하기 위한 제 개인적인 용어입니다.
* 다음번 게재할 글에서는 음정에 대해 추가적인 이야기와 여러 음정을 실제로 들어보고,
어떤 음정 관계인 음이 "깨끗하게" 들리는지, "불안하게" 들리는지 등등 이야기하겠습니다.
* 읽어 주셔서 감사합니다.
다음 시간으로 가기 Orpheus의 기초음악이론 2. - 음정(2) "자리바꿈 음정의 계산" 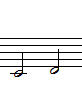




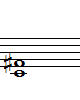
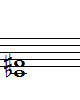


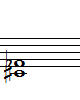


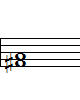

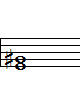
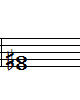
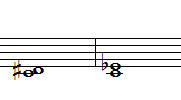

![]()