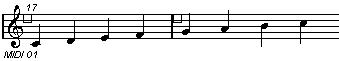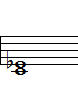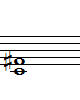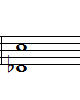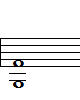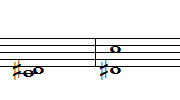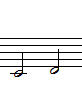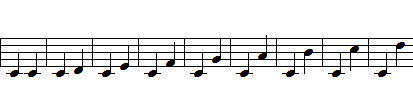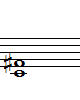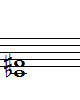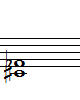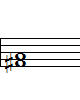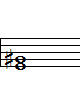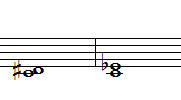Auditus

    전 시간으로 가기 Orpheus의 기초음악이론 8. - 화성(4) "4화음(1)"
다음 시간으로 가기 Orpheus의 기초음악이론 10. - 화성(5) "연습 문제"

화성 (4) "4화음(2)"


* 마우스를 악보에 올리시면 악보에 대한 설명이 보여지거나 또는 악보가 연주됩니다.


1. Diminished chord
 
 클래식 계열과 대중음악 계열에서의 diminished chord는 약간의 차이가 있습니다.
 클래식 계열에서의 diminished chord 는 감 3화음을 주로 얘기하는 것이고,
 대중음악 계열에서 diminished chord 는 감 4화음을 의미합니다.

 클래식 계열에서의 diminshed chord (감3화음)는 대중음악계열에서는 거의 나오지
 않습니다. 만약에 나온다면 표기는 "m-5"로 표시하는 것이 감7화음과 구별하는데 더
 편리하기에 "dim"표시 대신 "m-5"를 이용하시기를 추천합니다.

 클래식 계열에서의 diminished chord에 대한 설명은 다음 링크 
 Orpheus의 기초음악이론 6. - 화성(2) "3화음" , "화성의 자리 바꿈" 를 클릭하시거나

펼처보기

접기

2. 5음의 변형 형태 - 완전 5도의 기본형에서 증 5도 또는 감 5도 형태로

 minor chord 의 5도음이 반음 내려가서 감 5도가 되는 것을
 diminished (감) 코드라고 하겠죠? 표기는 "dim", 또는 "minor -5" 로 표시합니다.
   
   Cmin  chord : root - 단 3도 - 완전 5도
   Cm-5 chord : root - 단 3도 - 감 5도
   (단 3도음과 감 5도음 사이의 관계는 단 3도입니다. Root 에 단3 얹고 또 그 위에 단3)

 저번 시간에 나왔던 Bdim 코드를 Bm-5 로 표시해도 같다고 보시면 됩니다.
 그런데, 주의하실 점은 완전 똑같은 것은 아닙니다;;; 이 부분은 역시 저번에 말씀드린
 대로 다음 시간 이후에 설명하겠습니다.

접기

  Diminished 계열 중 4화음은 다음과 같습니다.  

표기	읽기 (종류)	구성음	음정
dim	디미니쉬드 (diminished)	C, Eb, Gb, Bbb	완전 1 + 단 3 + 감 5 + 감 7
m7-5	해프 디미니쉬드         (half diminished) 또는  마이너 세븐스 플래티드 피프쓰          (dominant 7th)	C, Eb, Gb, Bb	완전 1 + 단 3 + 감 5 + 단 7

 * Bbb 중 bb 는 더블플랫을 의미합니다.
 * m7-5 은 dominant 7th 계열이지만, 감3화음의 구성음(완전1 + 단3 + 감5)을 갖고
  있기 때문에 diminished 종류로 볼 수 있습니다. 그래서 half diminished 란 이름이
  붙습니다.
 * m7-5를 다시 설명하자면
  "m" 은 minor chord를 뜻함     :  단 3도음
  "7"  은 dominant 7th를 뜻함   : 단 7도음
  "-5" 은 완전 5도음의 b을 뜻함 : 감 5도음

 실제로 들어보고 그 차이를 구분해보도록 하겠습니다.
 (악보 위에 마우스를 올리면 악보가 연주됩니다.)

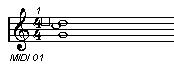
 1-1. Cdim (클래식 계열)   1-2. Cdim(대중음악계열)    1-3. Cm7-5
                                                         
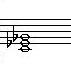
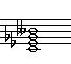
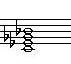
 귀로 듣고 그냥 흘려 보내버리지 마시고, 느낌들을 잘 기억해 주시면 좋습니다.
 대체적으로 다들 화를 내기 직전에 부들부들 떨고 있는 모습이랄까요;;;;
 흠.. 1-1. 클래식 계열의 감3화음은 남자분, 1-2.은 약간은 더 화려한 여자분, 같은 모습.
 그리고, 1-3.은 화를 잘 참지 못해서 감정의 편린이 삐져 나오는 사춘기? ^^;;;

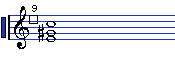
 그림의 1-2.는 다음 그림과 같이 b을 #으로 바꾸고 Bbb을 A음으로 표기하기도 합니다.
 다만, 정석(오르페우스의 정석?ㅋ)에 따르면 감화음이란 이름에 걸맞게 1-2.가 올바른
 표기이죠... 다만, 편리성과 시인성은 무시할 수 없어서 더 많이 이용됩니다~
     

 2-1. Cdim                    2-2. C#dim                  2-3. Ddim
      

         

          

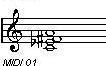
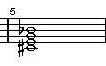
 2-4. Ebdim                  2-5. Edim                     2-6. Fdim
     

          

          

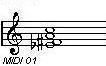
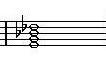
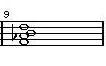
 2-7. F#dim                  2-8. Gdim                    2-9. G#dim
     

         

         

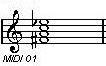
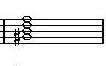
 2-10. Adim                  2-11. A#dim                2-12. Bdim
     

         

         

 
 
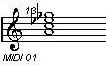
 세로줄을 열심히 보세요~ 제가 예전 강좌에서도 한 번 언급했을 겁니다.
 Cdim에서 C음을 자리바꿈하면 Ebdim가 됩니다. 이런 식으로 모두 따져보면,
 Cdim   = Ebdim = F#dim = Adim
 C#dim  = Edim  = Gdim  = A#dim, 그리고
 Ddim   = Fdim   = G#dim = Bdim 가 되므로 결국에 diminished chord 는 세 개만
 외우면 되는거죠... 기타 치시는 분들은 꼬~~옥 기억하세요!

 

2. 6th chord (3화음 + 장6도음)
 
 일반적으로, 6th chord는 재즈 계열에서 자주 나오는 chord입니다. 재즈 쪽에 관심이
 없으시더라도, 구성음의 전위(자리바꿈)을 함으로써, 다른 chord로 바꿔서 연주할 수
 있는 재밌는 chord이기 때문에 기타 연주하시는 분들은 알아두시면 편리합니다.

 6th chord는 주로 major나 minor의 3화음에 주로 붙여서 이용합니다.
 ex. C6 (C, E, G, A : 완전 1 + 장 3 + 완전 5 + 장6)
    Dm6 (D, F, A, B : 완전 1 + 단 3 + 완전 5 + 장6)

 6th chord는 따로 들려드려야 할 필요가 없습니다. 자리바꿈만 하면 지금까지 저희가
 배워온 chord에 다 포함이 되니까요~~ ^^

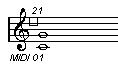
 3-1. major chord 의 6th chord = 한음 반 밑의 m7 chord
      

    악보 그림에서 알 수 있듯이 C6의 A음을 한 옥타브 밑으로 옮겨 주면 Am7이 됩니다.
    그러므로 6th chord가 m7chord의 느낌이 나겠죠?
    다만, 쓰임이나 연주 방법이 완전히 동일한 것은 아닙니다. 

    다 장조의 jazz 곡에서 C6를 Am7으로 쓰면 장조곡이 마치 단조처럼 보이거든요~
    그리고, 연주에 있어서 m7의 경우는 root 나 5음을 자주 생략하는데, roor가 빠지면,
    6th chord가 아닌게 되니까요... 흠... 자세한 설명은 나중으로 미루겠습니다;;;
    우선은 6th 가 무엇인지 아는게 중요하니까요!
    
    다만 6음을 자리 바꿈하면 1온음 + 1반음 밑의 m7으로 바뀐다는 정도만 기억하세요

 3-2. minor chord 의 6th chord = 한음 반 밑의 m7-5 chord
      

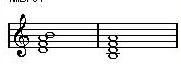
    이건 꼭 기억하셔야 합니다~ 보통 m7-5 를 연주 못하시는 분들이 많더라고요~
    Dm6의 6음인 B음을 한 옥타브 밑으로 옮기면 Bm7-5가 됩니다.

    Bm7-5의 표기만 봐도 굉장히 복잡해 보여서 무슨 코드인지 알려고 하지도 않고,
    대충 B7이나 Bm로 연주하면서 얼렁뚱땅 넘어가시는 분들 많이 봤습니다;;;;

    차라리 공식을 외워서 조금 더 쉽게 생각하세요~

    이건 역으로 생각하는 게 좋습니다.
    "m7-5가 나오면 1온음 + 1 반음 위의 m6로 바뀜"!!
    1온음 + 1반음은 쉽게 계산되시죠? A->C, B->D, D->F, E->G 정도야 쉽죠~
    피아노 건반만 머릿속에 바로 떠올리시면 됩니다. 

    * Bm7-5 는 Dm6 로 바꿔서 연주할 수 있다~ Dm6도 모르겠다면 걍 Dm~
    * 다 장조에서 Bm7-5를 Dm계열이나 G7으로 대신 연주가 가능한 것은 대리 코드에 
      관련된 이야기입니다~ 이것도 다음에 설명하겠습니다.
    

   전 시간으로 가기 Orpheus의 기초음악이론 7. - 화성(3) "코드의 진행(1)"
다음 시간으로 가기 Orpheus의 기초음악이론 9. - 화성(4) "4화음(2)"

화성 (4) "4화음(1)"


* 4화음을 이용하는 이유는 음의 울림이 더욱 풍부해지기 때문입니다.(재즈/팝)
  3화음만을 이용하여 곡을 쓰는 경우는, 곡이 깔끔하게 됩니다.(동요)

* 마우스를 악보에 올리시면 설명을 볼 수 있거나 악보가 연주됩니다.


1. 7th chord
 
 이름에서도 알 수 있듯이, Root 로부터 7도인 음을 3화음에 더한 것입니다.

 코드들에
 7th chord 는 다음 계열들로 이루어져 있습니다.
 1. Dominant 7th chord : 3화음 + 단 7 도의 음
 2. Major 7th       chord : 3화음 + 장 7 도의 음
 3. Diminished     chord : 감3화음 + 감 7 도의 음 


 다 장조에서 각각의 3화음들에 7th 음을 더해서 들어볼까요?
       
       

 1. Dominant 7th : Dm7, Em7, G7, Am7, Bm7-5
 2. Major 7th       : Cmaj7, Fmaj7

 위에서 알 수 있듯이 dominant 7th가 5개, major 7th가 2개입니다. dominant 7th
 (단 7도)가 훨씬 더 많기 때문에 이름에서 "dominant"를 생략하고 "7"만 붙여줍니다.

 Dm7 은 Dm chord (D,F,A)에 단 7도를 붙여준거고, (완전 1 + 단 3 + 완전 5 + 단7)
 G7 은 G chord (G,B,D)에 단 7도를 붙여준것입니다. (완전 1 + 장 3 + 완전 5 + 단7)
 
 major 7th (장 7도)는 "maj7"이라고 붙여줍니다. 
 Cmaj7 은 C chord (C,E,G)에 장 7도를 붙여줍니다. (완전 1 + 장 3 + 완전 5 + 장7)



 dominant 7th 와 major 7th 는 다음 예들처럼 거의 어떤 3화음에나 붙일 수 있습니다.
 

 그렇다면, dominant 7th 와 major 7th 의 소리는 어떻게 차이가 날까요? 

 C7 과 Cmaj7 을 들어보면서 알아보겠습니다.
                
 C7 은 약간 뭉쳐있고 긴장된 느낌, Cmaj7 은 건조하고 쌀쌀한 느낌 정도일까요? 
 여러분도 각자 느끼시는 대로 이미지화해서 기억해 두세요~~
 
 C7 과 Cmaj7 에서 7음을 한 옥타브 낮춰서 Root 음인 "C"음 아래에 2도 관계가 되로록
 놓겠습니다.
                 
 
  C7 에서 Bb 과 C 음 사이는 장 2도 음정 관계입니다.
  Cmaj7 에서 B 와 C 음 사이는 단 2도 음정 관계입니다.
  그래서, 약간 더 안정적으로 들리는 소리는 C7 이 되겠죠?
  Orpheus의 기초음악이론 4. - 음정(4) "귀로 들어 보는 음정의 울림" 를 공부하셨던
  분들은 쉽게 이해하실 수 있을 겁니다. 음정 관계에 따라서 어떻게 들리는지 아직 잘
  모르시는 분은 다음 "더보기"를 클릭하셔서, 소리를 마음에 느껴보세요;;;;;

더보기

접기

* 마우스를 그림에 올리면 소리가 들립니다.


        (1) 단 2 도         (2) 장 2 도         (3) 단 3 도         (4) 장 3도
                             

        (5) 완전 4 도      (6) 증 4 도         (7) 완전 5 도      (8) 단 6 도
                             

        (9) 장 6 도       (10) 단 7 도        (11) 장 7 도      (12) 완전 8 도
                             

제 귀에는     완전 8도가 제일 무난하게 들립니다.
그 다음에는  완전 4도, 완전 5도인데 5도가 4도보다 약간 밝게 들립니다.
그 다음에는 장 3도, 단 6도, 단 3도, 장 6도 정도가 안정적으로 들리고,
그 다음에는 장 2도, 단 7도~~
마지막으로는 증 4도, 단 2도, 장 7도인데 단 2도가 더 지저분하게 들리네요~~

접기

   전 시간으로 가기 Orpheus의 기초음악이론 6. - 화성(2) "3화음" , "화성의 자리 바꿈"
다음 시간으로 가기 Orpheus의 기초음악이론 8. - 화성(4) "4화음" 

화성 (3) "코드의 진행(1)"


* 이번 시간에는 기본적인 코드 진행과 곡의 진행에서 화성의 자리바꿈꼴의 의미를 생각해
  보는 시간입니다. 

* 마우스를 악보에 올리시면 설명을 볼 수 있거나 악보가 연주됩니다.


1. 코드 진행의 표기
 
 코드 진행을 표기할 때는 "-" 과 간격으로 간단히 표시가 가능합니다.

 "-"   : 화살표, 즉 진행의 의미
 간격 : 마디를 의미

 Ex. 1 :  C     -  F        -  G     -  C  : C, F, G, C 코드 순서대로 한마디씩 연주
 Ex, 2 :  C     -  Dm-F -  G     -  C  : C 한 마디, Dm, F는 반마디씩, G, C는 한마디씩
 Ex. 3 :  C     -  C        -  F     -  C  : C 두 마디, F 한 마디, C 한 마디 연주  


2. 코드 진행 - 마침 (Cadence)

 코드 진행에서 우선적으로 알아두어야 할 것은 "한 소절이나, 음악 전체의 끝은 어떻게
 끝나는가?"입니다. 중고등학교때, 배운 가장 기본적인 마침꼴의 형태는 다음과 같습니다.


  그림 1-1 . 바른 마침 (Authentic cadence) : V - I
  
   
  그림 1-2. 벗어난 마침 (Plagal cadence)   : IV - I (일명 Amen cadence : 아멘 마침)
 >

 
 그런데, 왜 이렇게 끝나는게 좋을까요? 그 이유에 대해서는 아무도 설명안해줍니다 ㅡ_ㅡ
 
 그에 대한 제 의견입니다.
 앞선 시간에 음정에 대한 설명들이 있었죠?
 두 음 사이의 음정 중 가장 안정된 형태는 완전 4도 관계과 완전 5도 관계였습니다. 
 
 그림 1-1. 과 1-2. 에서 각각의 코드들에 대한 음정을 계산하는 것이 아니라,
 G - C 로 또는 F - C 로 연결되는 선율적 음정들을 계산해 보세요... 
 
  G  →  C ( V - I )                                 F  →  C   ( IV - I )
  솔 → 도   : 완전 5도 관계                     파  →  도   : 완전 4도 관계
  시 → 미   : 완전 5도 관계                     라  →  미   : 완전 4도 관계
  레 → 솔   : 완전 5도 관계                     도  →  솔   : 완전 4도 관계 

 음악에서 그 음악의 조성 (Key)를 확실하게 해 주는 것은 I 도의 코드입니다.
 일반적으로 한 곡의 끝마디는 I 도로 끝나게 됩니다. 그리고, 끝나는 I 도를 안정적으로
 꾸며주는 것은 위에서 확인했다시피, 음정에서 가장 완벽한 완전 4도나 5도의 음입니다.

 그래서, 코드 진행도 V - I 이나, IV - I 의 형태로 되는 것입니다.



3. 곡의 진행에서 코드의 자리바꿈
 
  보통 일반적으로 연주할 때 자리바꿈하는 이유를 "연주가 편하기 때문에"로 생각하시는 
  분들이 많습니다.... 그렇지만, 그것은 절대 주목적이 아닌 부가적인 이득일 뿐입니다.
  자리바꿈의 목적은 진행을 부드럽게 하기 위함입니다.

  음의 진행에서 순차진행과 도약진행이라는 것이 있습니다.
  순차진행은 앞의 음과 뒤의 음 사이가 2도 관계 음정이 되게끔 음이 움직이는 것이고,
  도약진행은 그 이외라고 생각하시면 됩니다.

  비유를 들자면 
  순차진행은 가만히 서 있다가 천천히 걷는 것, 도약진행은 가만히 서 있다가 갑자기 뛰는
  것이라고 생각하면 됩니다. 당연히 순차진행이 안정적이고 부드러운 거죠...
  반면에 도약진행은 역동적이고, 거칠게 됩니다.

  다음 그림에서 확인하겠습니다. 똑같은 V - I 임에도 V의 자리바꿈꼴인 그림 2-2.의
  흐름이 더 부드럽게 들립니다. 
  그 이유는 도약진행이 아닌 순차진행을 했기 때문입니다.

  앞에서도 말씀드렸지만, 다시 한번 강조합니다. 절대절대 "연주가 편해서 자리바꿈한다"
  라는 생각은 안 하시는 것이 좋습니다. 만약 역동적인 곡에서라면 그림 2-2. 형태보다는
  오히려 그림 2-1 같은 형태가 더 좋을 수도 있기 때문입니다.

그림 2-1 . 바른 마침 (Authentic cadence) : V - I
  

 그림 2-2 . 바른 마침 : V - I    ( V 도의 자리바꿈꼴)
  



4. 5도권의 진행
  
  "코드진행 - 마침"에서도 설명했듯이 앞의 코드는 뒤의 코드의 4도나 5도 관계인 
  것이 제일 안정적입니다. 그렇다면 5도 관계로 계속 코드를 나열하면 어떻게 될까요?

  5도 상승 (=4도 하강)
  C → G → D → A → E → B → F# → C# → G# → D# → A# → F → C

  5도 하강 (=4도 상승) - 위와 역순입니다.
  C → F → Bb → Eb → Ab → Db → Gb → B → E → A → D → G  → C 

  위와 같은 흐름이 나오겠죠? 가장 안정적인 형태의 흐름이 완성됩니다. 그렇지만, 이것을
  그대로 이용하기보다는 응용해서 이용하는 편이 좋습니다. 왜냐면, C, F, G 코드를 제외
  하면 다장조에서는 그냥 나올 수 있는 화음들이 아니죠? 그래서 그냥 이용하려고 하면,
  곡을 진행해나가기가 상당히 힘듭니다.
 
  가령 C maj (다장조) 로 음악을 만들려고 한다면 다음 과정과 같이 변형합니다. 
  1. C G D A 만 따온다.
  2. D 와 A 는 다 장조에서 나올 수 없는 코드이므로 각각 Dm 와 Am 로 변형한다.

  위와 같은 과정을 거치면 C - G - Dm - Am 로 진행되는 코드를 이용하여 곡을 진행해
  나갈 수 있습니다. 뭔가 썰렁하고 허전해도 다음처럼 말이죠;;;

  

클릭해서 보세요~

   전 시간으로 가기 Orpheus의 기초음악이론 5. - 화성(1) "코드의 형성" 
다음 시간으로 가기 Orpheus의 기초음악이론 7. - 화성(3) "코드의 진행(1)" 

화성 (2) "3화음", "화성의 자리 바꿈"


* 저번 시간에 배운 코드의 형성 이론에서는 3음이 변형되는 형태에 따라 코드의 이름이
  바뀐다는 것을 이해하셨을 거라고 생각합니다. 이번 글은 5음이 변형되는 형태도 설명
  할까 합니다.
 

1. 3음의 변형 형태 복습

 Root - 장 3도    - 완전 5도 : major(장) 코드
 Root - 단 3도    - 완전 5도 : minor(단) 코드
 Root - 완전 4도 - 완전 5도 : suspended 코드

 C chord 를 "씨 메이저 코드"라고 읽기도 합니다. 그렇지만, 실제 표기에서는 일반적으로
 major 나 maj 를 붙이지 않습니다. 가장 기본적인 코드라서 생략하기도 하고,  4화음을
 표기할 때 다른 의미와 중복되어버리기도 해서 생략합니다.
 이 부분은 다시 4화음 들어갈 때 설명하겠습니다.


 가장 기본적인 C, Cm, Csus4 등을 실제로 들어보겠습니다.

     

 Cmajor 는 밝은 느낌, Cminor 는 어두운 느낌, Csus4는 긴장된 느낌인가요?



2. 5음의 변형 형태 - 완전 5도의 기본형에서 증 5도 또는 감 5도 형태로

 major chord 의 5 도음이 반음 올라가서 증 5도가 되는 것을
 augmented("증"이란 의미)코드라고 합니다. 표기는 "aug", 또는 "+5" 로 표시합니다.
   
   C       chord : root - 장 3도 - 완전 5도
   Caug chord : root - 장 3도 - 증 5도
   (장 3도음과 증 5도음 사이의 관계는 장 3도입니다. Root 에 장3 얹고 또 그 위에 장3)

 minor chord 의 5도음이 반음 내려가서 감 5도가 되는 것을
 diminished (감) 코드라고 하겠죠? 표기는 "dim", 또는 "minor -5" 로 표시합니다.
   
   Cmin  chord : root - 단 3도 - 완전 5도
   Cm-5 chord : root - 단 3도 - 감 5도
   (단 3도음과 감 5도음 사이의 관계는 단 3도입니다. Root 에 단3 얹고 또 그 위에 단3)

 저번 시간에 나왔던 Bdim 코드를 Bm-5 로 표시해도 같다고 보시면 됩니다.
 그런데, 주의하실 점은 완전 똑같은 것은 아닙니다;;; 이 부분은 역시 저번에 말씀드린
 대로 다음 시간 이후에 설명하겠습니다.

 
3. 코드의 자리 바꿈꼴들
 클랙식에서는 전위라는 말을 쓰기도 하지만 우리는 조금 쉽게 말하죠~
 C, E, G 음으로 구성된 코드라면 C chord 이죠~ 그런데, 다음 그림처럼 E, G, C 로
 구성된 코드나 G, C, E 로 구성된 코드는 무엇이라고 불러야 할까요?
 

 C chord 와 구성음은 같기 때문에 둘 다 C chord 입니다. 다만, 맨 밑에 오게 되는 음이
 다르죠? 이 때, 맨 밑의 음을 Bass note 라고 하고, 표기는 다음과 같이 합니다.
 
 "Chord name" on "Bass note"
 ex) C on E (C chord 이지만 bass note 음이 E 음이다.)
       C on G (C chord 이지만 bass note 음이 G 음이다.)

 각 코드를 구성하는 음이 무엇인지 전부다 기억하고 힘들다면 4도 관계가 보이는 음을
 한 옥타브 위나 밑으로 옮겨보면 전부다 3도 관계가 나오는 것을 보고 파악하는 방법도
 있습니다.

 피아노나 기타 연주 악보를 보다 보면 저런 식으로 쓰여져 있는 것들 많이 보셨을 겁니다.
 일반적으로는 둘 다 "C" 로만 표기해도 되지만, on "bass note" 를 붙여 쓰는 이유와
 표기가 안 되어 있어도 저런 식으로 자리바꿈까지 해주는 게 좋은 이유는 다음 시간을
 기대해 주세요~ 마지막으로 연습문제들을 올려놓겠습니다~~~


4. 연습 문제 (마우스를 올리시면 코드 명칭이 나옵니다. 풀고 맞춰 보세요~)

  연습 4.                           연습 5.                           연습 6.

  연습 7.                           연습 8.                           연습 9.

  연습 10.                          연습 11.                          연습 12.

연습문제 9와 10은 구성음이 같죠? Caug = E aug = G#aug 인 관계가 성립합니다.



  

   전 시간으로 가기 Orpheus의 기초음악이론 5. - 화성(1) "코드의 형성" 
다음 시간으로 가기 Orpheus의 기초음악이론 7. - 화성(3) "코드의 진행(1)"

Orpheus의 기초음악 이론을 시작하며...

(1) 내 스스로는 내가 지금까지 알고 있는 지식들을 정리하며
(2) 또 제 블로그에 찾아주신 여러분들께는음악을 연주하거나 MIDI를 접하게 되면서,
       연주, 작곡, 편곡을 해나갈때 도움이 되었으면 하는 바람으로 시작합니다.
(3) 음악 비전공자이기 때문에 내용상 틀린 부분이 있을 수 있습니다. 피드백 부탁드립니다.
(4) 악보 그림위에 마우스를 올리거나, 클릭하면 악보의 연주 또는 악보의 설명이 있습니다.
 
 

 다음 시간으로 가기 Orpheus의 기초음악이론 2. - 음정(2) "자리바꿈 음정의 계산"      


음정 (1) "음정의 정의와 계산"


1. 음정이란?
    - 정의           : 악보 표기 상에서 한 음과 다른 음 사이의 음높이의 차이
    - 선율적 음정 : 순차적으로 소리가 나는 경우의 음정
    - 화성적 음정 : 동시에 소리가 나는 경우의 음정
     
                                
            그림 1-1.  선율적 음정       그림 1-2. 화성적 음정
                              

2. 음정의 계산 방법
  (1) 첫 단계
     - 무조건 다장조로 생각하기 (무조건 # 이나 b 없애기)
     - 동일 음정은 1도, 악보 상에서 차례대로 1도씩 증가.
     - 두 음 중 아래쪽에 있는 음을 기본으로 계산하기
     
        그림 2-1.

                                 #이나 b이 없다면 모두 "도~레" 로 생각할 수 있으므로 전부 2도 관계임    

  (2) 두번째 단계
     - 완전, 장, 단, 증, 감이란 말 붙여보기
     - 이를 위해서는 우선 다장조에서 기본음인 "도"를 중심으로 알아보기

            완전 1도  장 2도  장 3도  완전 4도  완전 5도  장 6도  장 7도  완전 8도  장 9도      

            * 1 2 3  4 5  6 7    의 앞에 말을 붙이면
            * 완장장 완완 장장   이 됩니다.
            * 세로줄로 읽으면 1완 -> 즉, 완전 1도
                                      2장 -> 즉, 장 2도
            * 도~파의 계산은 도부터 따져서 레(2도), 미(3도), 파(4도) 이므로 4도 관계이고,
                1 2 3  4
                완장장 완 이므로 완전 4도가 됩니다.
            * 8도를 넘어가도 완장장~~~~ 식으로 나간다고 생각하면 완전 8도, 장9도가 됩니다.


  (3) 세번째 단계
     - 완전, 장에서 온음과 반음이 각각 몇개씩인지 알아보기
     - 온음 한개는 반음 두개가 합쳐진 것과 같습니다.
     - "미~파" 사이는 반음 1개로 진행, "시~도"사이도 마찬가지로 반음 1개로 진행됩니다.

        표 1.
                 * 음정        온음 개수       반음 개수     sum : 온음을 2, 반음을 1로 계산하면
         도도       완전 1도           0                   0                  0
         도레          장 2도           1                   0                  2
         도미          장 3도           2                   0                  4
         도파       완전 4도           2                   1                  5
         도솔       완전 5도           3                   1                  7
         도라          장 6도           4                   1                  9
         도시          장 7도           5                   1                 11
         도도       완전 8도           5                   2                 12

 
  (4) 네번째 단계 (Final)
     - 완전, 장, 단, 증, 감, 겹증, 겹감의 관계 알아보기
     - 완전 1,4,5,8 도에서는 두 음 사이의 거리가 반음만큼 더 멀어지면 "증",
                                                               반음만큼 더 가까워지면 "감"이됩니다.

        표 2.
    sum의 변화  
        또는                               -1       -1        +1      +1    
  반음 개수의 변화
                                    겹감 <-- 감 <-- 완전 --> 증 --> 겹증



                            
        그림 2-2.     감 4도            완전 4도            증 4도            겹증 4도
                      (반음 좁아짐)                            (반음 멀어짐)  (증 4도에서 또 반음 멀어짐)

       

         예제 2-1. (답은 그림에 마우스 올리시면 나타납니다.)


   
  - 장 2,3,6,7 도에서는 두 음 사이의 거리가 반음만큼 더 멀어지면 "증",
                                                              반음만큼 더 가까워지면 "단"이됩니다
  - 단 2,3,6,7 도에서는 두 음 사이의 거리가 반음만큼 더 멀어지면 "장",
                                                              반음만큼 더 가까워지면 "감"이됩니다


        표 3.
    sum의 변화  
        또는                              -1       -1                  +1      +1    
  반음 개수의 변화
                                    겹감 <-- 감 <-- 단 <--> 장 --> 증 --> 겹증

        그림 2-3. (1) 파~라 이므로 우선 3도 관계의 음
                      (2) 파~솔, 솔~라 사이는 각각 온음 하나씩 움직인다.
                           그러므로 파~라까지는 온음 2개이므로, 표1에 의해 파~라는 장3도이다.
                      (3) 위의 음 라에 #이 붙어서 반음만큼 사이가 멀어지므로 증 3도이다.

        그림 2-4. (1) 미~솔이므로 우선 3도 관계의 음
                      (2) 미~파는 반음, 파~솔은 온음으로 움직인다.
                           표1. 에 의해 장 3도는 온음이 두개일 때이다. 그런데,
                           반음만큼 두 음 사이가 가까워졌으므로, 단 3도

        예제 2-2. (답은 그림에 마우스 올리시면 나타납니다.)

        예제 2-3. (답은 그림에 마우스 올리시면 나타납니다.)


  (5) 이명동음적 음정
   
                                           
        그림 2-4.  레# 과 미b은 실제로 같은 소리가 나는 음이다.
                      다만 악보상에서 "도~레#" 과   "도~미b"은 다른 음정이다.
                      도~레# : 증 2도
                      도~미b : 단 3도


  - 표 1. 을 다시 한 번 확인해 보자.
  - 장 2도는 sum 이 2, 반음만큼 사이가 더 늘어난 증 2도는 2 + 1 을 해서 sum3 이 된다.
  - 장 3도는 sum 이 4, 반음만큼 사이가 더 줄어든 단 3도는 4 - 1 을 해서 sum3 이 된다.
  - 이렇게, 다른 이름의 음정을 같고 있지만, 실제 연주에서 같은 음이 나오게 되는 음정을
    이명동음적 음정이라고 한다.
               
        표 1.
                 * 음정        온음 개수       반음 개수     sum : 온음을 2, 반음을 1로 계산하면
         도도       완전 1도           0                   0                  0
         도레          장 2도           1                   0                  2
         도미          장 3도           2                   0                  4
         도파       완전 4도           2                   1                  5
         도솔       완전 5도           3                   1                  7
         도라          장 6도           4                   1                  9
         도시          장 7도           5                   1                 11
         도도       완전 8도           5                   2                 12


3. 문제
  (1) 다음 두 음의 음정을 계산하시오.

  (2) 다음 두 음의 음정을 계산하시오.

* 본문 중의 "sum"이라는 용어는 음정 관계를 수적으로 표현하기 위한 제 개인적인 용어입니다.
* 다음번 게재할 글에서는 음정에 대해 추가적인 이야기와 여러 음정을 실제로 들어보고,
  어떤 음정 관계인 음이 "깨끗하게" 들리는지, "불안하게" 들리는지 등등 이야기하겠습니다.
* 읽어 주셔서 감사합니다.